Applied Math with JavaScript — How Pythagoras is essential for advanced programming

Down to the most fundamental level, code is abstract math. If you want to maximize your potential of writing performant and flawless code, or if you want to explore the new frontiers of programming, where its no longer possible to simply plug in a library and call it a day, upping your math skills is essential.
In this article series, we are going to explore concepts where the fundamental mathematical principles are the guiding force.
The distance formula
Derived from the pythagorean theorem, the distance formula is a definitive fundamental unit in computer science, used in everything from games, machine learning to search engines. Having a clear understanding of how it works is essential.
Examples could be measuring the distance between two players in a game, calculating the error rate between the expected result and output of a deep learning system, or performing advanced text search by vectorizing the input and comparing it to similar strings. The distance formula is the basic unit for all of these systems where you would like to make sense of multi-dimensional data.
So let's start by dissecting the pythagorean theorem. The theorem tells us that if we have a right-angled triangle with all sides known except for the hypotenuse c, we can calculate it using the two other sides a and b.
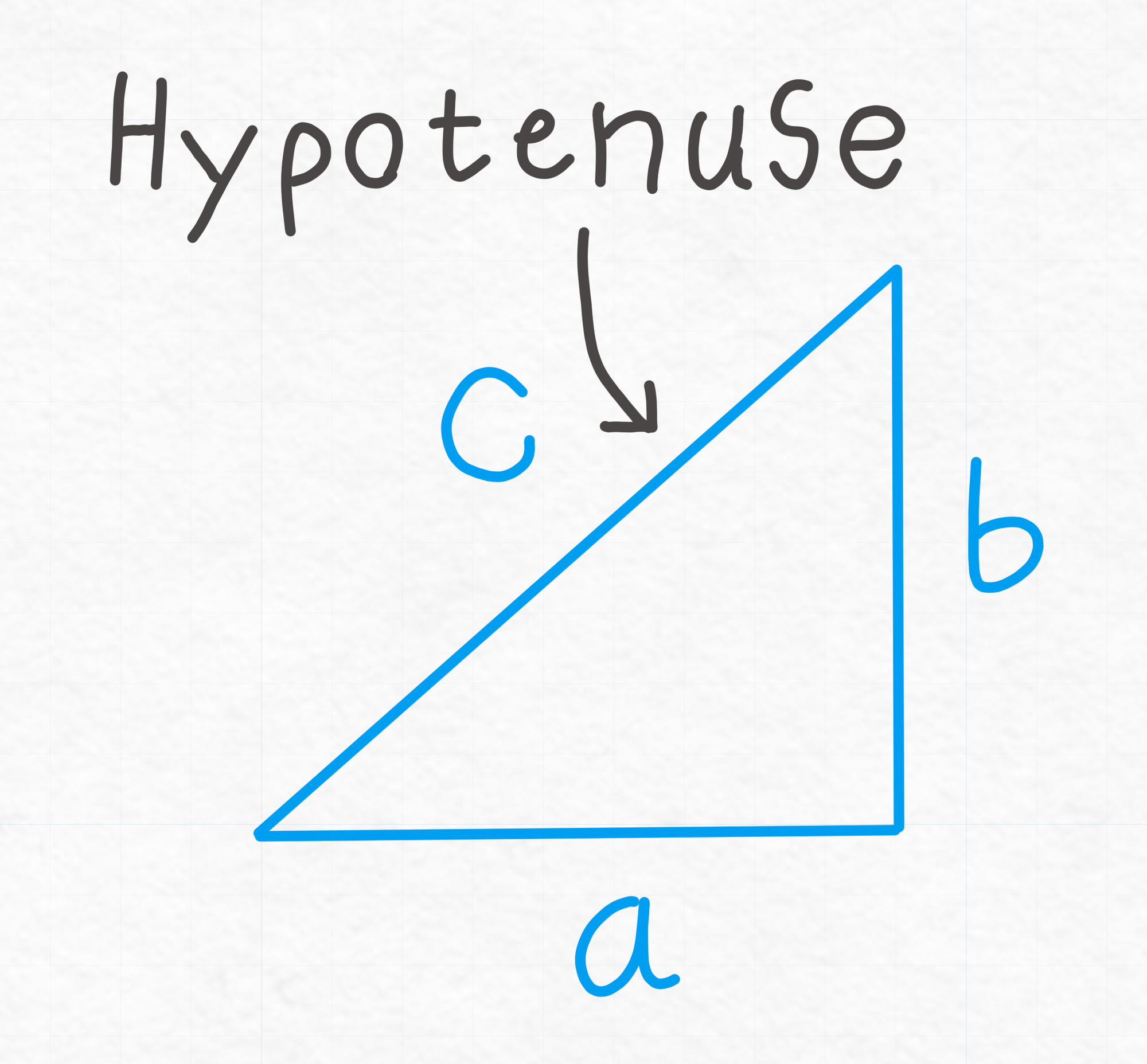
Meaning the triangle is represented as:

And if the lengths of both a and b are known, then c can be calculated as:

The distance formula builds on this principle. It can be illustrated as subtracting one triangle from another, and then applying the pythagorean theorem on the resulting triangle to find the length of the resulting hypotenuse.
Instead of looking it at as simply a triangle, we can look at the "triangle" as a point on a plane by defining side a as the vector component along the x-axis, and b as the vector component along the y-axis.
In the first illustration we define two points, P0 and P1, and by tracing the x and y-axis, we can define a triangle for each of them.
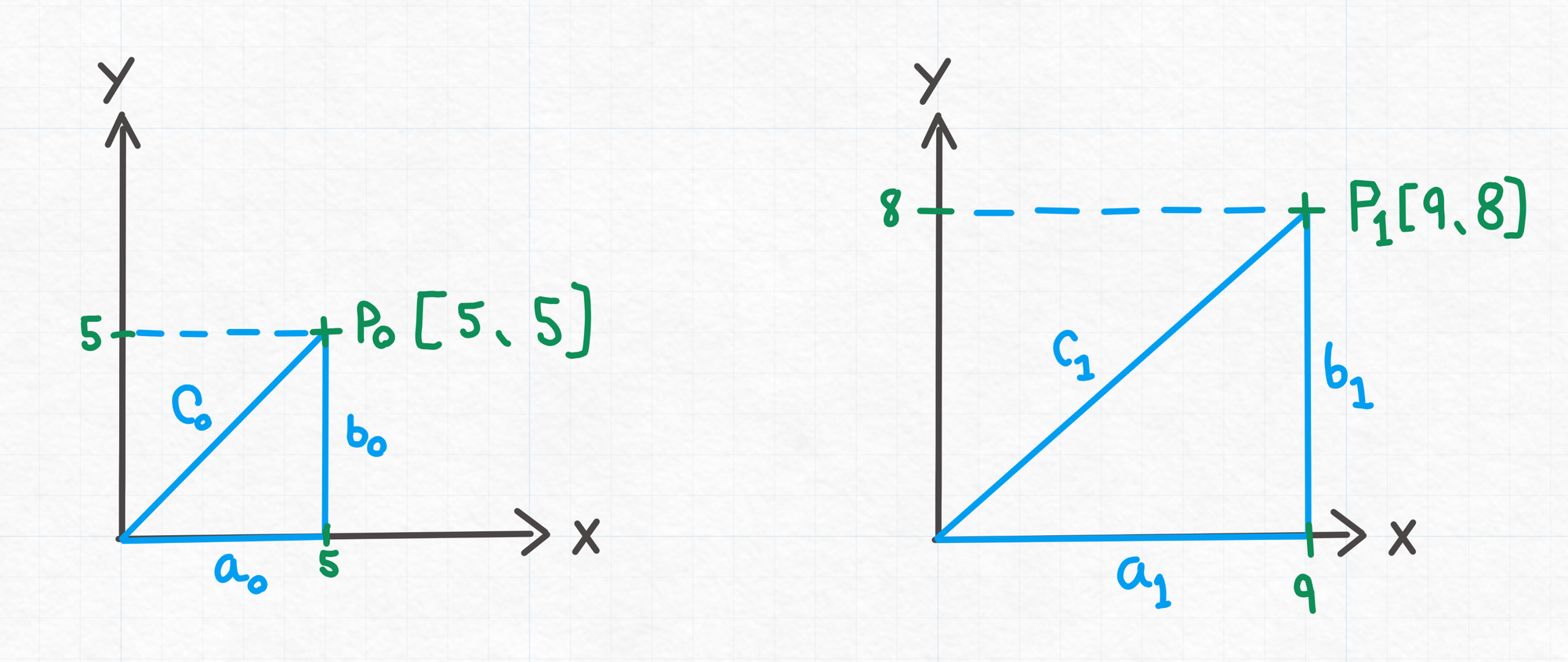
Next we subtract P0 from P1, and can see how the resulting triangle illustrates the directional vector from P1 to P0.
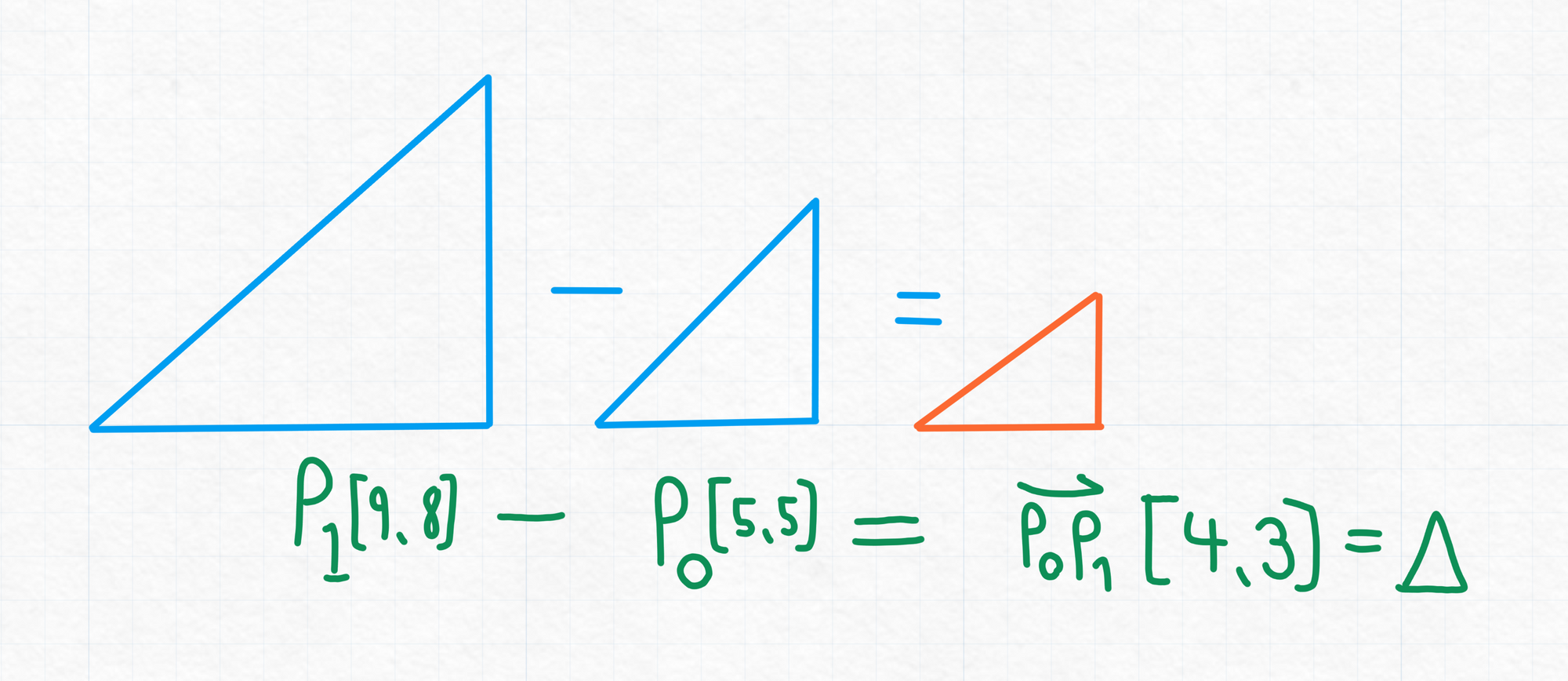
In the final step we use pythagoras to calculate the length of the resulting hypotenuse, this is the distance between the two points.
In the illustration below you can see how the resulting triangle fits snugly between P0 and P1 if we offset it with the components from P0. With the a component as the distance along the x-axis, the b component as distance along the y-axis, and the hypotenuse c as the actual distance between the two points.

This simple principle can be expanded to get the distance between vectors of any dimension, shown in the code examples below.
Code Examples
I have added some code examples and tasks here, you can click on "Edit on Codepen" to experiment with the code and solve the tasks!
Related Insights
Since we multiply each vector component by itself in the pythagorean theorem, the resulting value will always be positive, making the sign of the component irrelevant.
The operation of multiplying each component of a vector by itself and then summing up the result can be represented as a dot product, meaning if you have access to a numeric / simd vector library you can get some decent performance improvements by using a dot product on the directional vector by itself, and then calculating the square root of the result.
Knowledge retention
If you found this article useful, you might want to consider storing it somewhere you will find it the next time you are working on something related. A Emberly topic is ideal, but as a non-paid solution, a bookmark manager, Trello card or a google docs works just fine as well!
References:
1: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Array/Reduce
2: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Array/map

